 |
Применение машинного обучения для поиска свойств атомарных геометрических фигур показывает, как искусственный интеллект способен ускорить открытия в математике. Математики из Имперского колледжа Лондона и Ноттингемского университета впервые использовали машинное обучение для расширения и ускорения работы по выявлению атомарных форм, которые образуют основные части геометрии в высших измерениях. Результаты исследования опубликованы в журнале Nature Communications. По мнению авторов, использование искусственного интеллекта в форме машинного обучения может изменить подход к математике. Доктор Александр Каспшик из Ноттингемского университета сказал:
Профессор Том Коутс с кафедры математики Имперского университета добавил:
Аспирантка Сара Венесиале (Sara Veneziale) с кафедры математики Imperial сказала:
Определение фигурМатематики описывают формы с помощью уравнений и, анализируя эти уравнения, могут разложить форму на фундаментальные части. Эти части, эквивалентные атомам, являются строительными блоками фигур и называются многообразиями Фано. Группа специалистов из Имперского университета и Ноттингема начала составлять «периодическую таблицу» этих разновидностей Фано несколько лет назад, но найти способы их классификации по группам с общими свойствами оказалось непросто. Теперь, используя машинное обучение, они выявили неожиданные закономерности в многообразиях Фано. Одним из аспектов многообразия Фано является его квантовый период — последовательность чисел, которая действует как штрих-код или отпечаток пальца. Было высказано предположение, что квантовый период определяет размерность многообразия Фано, однако до сих пор не было теоретического предложения, как это работает, и не было возможности проверить это на огромном наборе известных многообразий Фано. Машинное обучение, однако, создано для поиска закономерностей в больших массивах данных. Обучив модель машинного обучения на некоторых примерах данных, команда смогла показать, что полученная модель может предсказывать размеры многообразий Фано по квантовым периодам с точностью 99%. Кодирование реального мираМодель искусственного интеллекта не позволяет с уверенностью утверждать, что открытие состоялось, поэтому для доказательства того, что квантовый период определяет размерность, они воспользовались более традиционными математическими методами, используя для этого модель искусственного интеллекта. Помимо использования машинного обучения для открытия новой математики, команда утверждает, что наборы данных, используемые в математике, могут помочь в совершенствовании моделей машинного обучения. Большинство моделей обучаются на данных, взятых из реальной жизни, таких как медицинские или транспортные данные, которые по своей природе являются «шумными» — они содержат много случайностей, которые в некоторой степени маскируют реальную информацию. Математические данные являются «чистыми» — без шумов — и содержат закономерности и структуры, лежащие в основе данных и ожидающие своего раскрытия. Поэтому такие данные можно использовать в качестве полигона для тестирования моделей машинного обучения, улучшая их способность находить новые закономерности. 04.10.2023 |
Net&IT
 | |
| Учёные ЛЭТИ создали прототип системы для прогноза осадков и диагностики фруктов | |
Прототип интеллектуальной системы в будущ... | |
 | |
| Казанский студент намерен разработать умные очки в 3 раза дешевле аналогов | |
Осман Ширгалин, студент 2 курса Института вычи... | |
 | |
| Прекратите гуглить и поспите днем, чтобы снизить риск деменции | |
Канадский учёный Мохамед И. Элмасри считает, ч... | |
 | |
| AIChE Journal: Инженеры исследуют расширение интеллекта для большей безопасности | |
В последние годы искусственный интеллект стал ... | |
 | |
| Эффективность светодиодов для дополненной реальности выросла вдвое | |
Учёные из России и Кореи усовершенст... | |
 | |
| App.System Innovation: Управлять умными колонками оказалось слишком сложно | |
Благодаря удобству и возможности управлят... | |
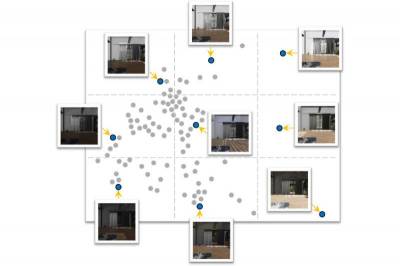 | |
| Patterns: Детский зрительный опыт поможет усовершенствовать компьютерное зрение | |
Новый подход к обучению систем искусствен... | |
 | |
| ИИ-платформа для анализа изображений поможет развивать исследования во всем мире | |
Группа исследователей из Института Гульбе... | |
 | |
| Инженеры воссоздали голопалубу Star Trek с помощью ChatGPT и видеоигр | |
В сериале Звездный путь: Следующее поколение к... | |
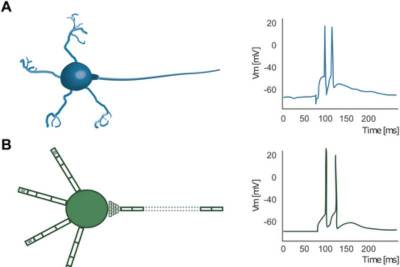 | |
| IC: Исследователи тестируют биологическую безвредность нейроморфной сети | |
Биологический мозг, в особенности человеч... | |
 | |
| Science: Аналоговые вычисления дают решать сложные уравнения и экономят энергию | |
Группа исследователей, включая инженеров Масса... | |
 | |
| В 40% случаев люди ошибочно называют сгенерированное фото человека реальным | |
Если вам недавно было трудно понять, явля... | |
 | |
| Physical Review X: Сеть квантовых датчиков повышает точность измерений | |
Квантовые системы, используемые в квантов... | |
 | |
| Scientific Reports: ИИ показал больший творческий потенциал, чем человек | |
Еще один балл в пользу искусственного инт... | |
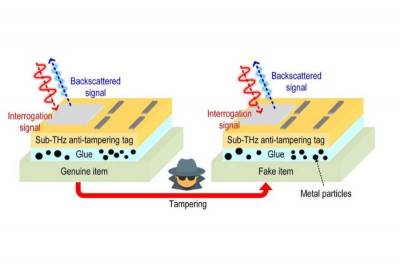 | |
| Крошечную метку на замену RFID сделали еще надежнее | |
Несколько лет назад исследователи Массачу... | |
 | |
| Привыкнув доверять, люди не поймут, когда ИИ начнет манипулировать | |
Согласно обширному обзору, в настоящее вр... | |
 | |
| Умные серьги с низким энергопотреблением будут измерять температуру по мочке уха | |
Умные аксессуары становятся все более рас... | |
 | |
| Для борьбы с бешенством разработали приложение для распознавания собачьих морд | |
Новое приложение для распознавания собачь... | |
 | |
| Генеративный ИИ помогает ученым объяснить человеческую память и воображение | |
Последние достижения в области генеративн... | |
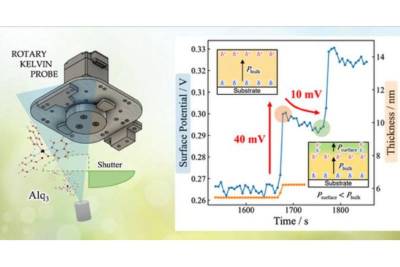 | |
| Ученые приблизились к более легким и гибким оптоэлектронным устройствам | |
Органические оптоэлектронные устройства, такие... | |
 | |
| ChatGPT перелопатил почти весь интернет, но пока не научился рассуждать | |
Языковые модели ИИ переживают бум. В ... | |
 | |
| Если сотрудникам скорой помощи поможет ИИ, они смогут спасать больше жизней | |
Чтобы определить, насколько серьезно пострадал... | |
 | |
| Беспроводная система отслеживания улучшит впечатления от расширенной реальности | |
Новая технология, разработанная инженерами Кал... | |
 | |
| PNAS Nexus: ИИ пока еще далеко до человеческих способностей мыслить | |
Атанасиос С. Фокас рассматривает актуальный во... | |
 | |
| Nature: ИИ генерирует белки с исключительной прочностью связывания | |
В новом исследовании, опубликованном 18 декабр... | |
 | |
| Nature Computational Science: ИИ может предсказывать события в жизни людей | |
Искусственный интеллект, разработанный для&nbs... | |
 | |
| Разработан фреймворк ИИ для определения новых показаний к применению лекарств | |
Ученые из компании Klick Applied Sciences... | |
 | |
| Искусственный интеллект отлично справляется с имитацией, но не с инновациями | |
Системы искусственного интеллекта часто изобра... | |
 | |
| Nature Electronics: Изменение памяти дает новые вычислительные возможности | |
Ученые Рочестерского университета разработали ... | |
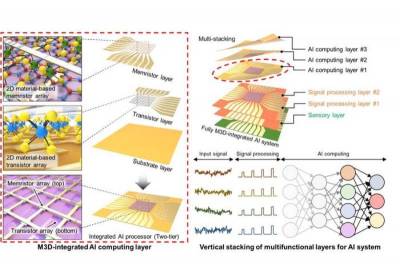 | |
| Nature: 2D-материал изменяет форму 3D-электроники для искусственного интеллекта | |
Многофункциональные компьютерные чипы эволюцио... | |