 |
Прогнозирование погоды важно для различных отраслей, включая сельское хозяйство, военные операции и авиацию, а также для предсказания стихийных бедствий, таких как торнадо и циклоны. Оно основано на прогнозировании движения воздуха в атмосфере, которое характеризуется турбулентными потоками, приводящими к хаотическим завихрениям воздуха. Однако точное предсказание этой турбулентности остается весьма сложной задачей из-за недостатка данных о мелкомасштабных турбулентных потоках, что приводит к появлению небольших начальных ошибок. Эти ошибки, в свою очередь, могут привести к резкому изменению состояния потока в дальнейшем — явление, известное как хаотический эффект бабочки. Чтобы решить проблему ограниченности данных о мелкомасштабных турбулентных потоках, для прогнозирования был использован метод, основанный на данных, известный как ассимиляция данных (DA). Интегрируя различные источники информации, этот подход позволяет получить подробные сведения о мелкомасштабных турбулентных вихрях на основе их более крупных аналогов. Примечательно, что в рамках методов DA был определен важнейший параметр, известный как критический масштаб длины. Этот критический масштаб длины представляет собой точку, ниже которой вся необходимая информация о мелкомасштабных вихрях может быть экстраполирована на более крупные. Число Рейнольда, показатель уровня турбулентности в потоке жидкости, играет ключевую роль в этом контексте: более высокие значения означают повышенную турбулентность. Однако, несмотря на консенсус, достигнутый в результате многочисленных исследований, относительно общего значения критической шкалы, объяснение ее происхождения и связи с числом Рейнольда остается неуловимым. Для решения этой проблемы группа исследователей под руководством доцента Масанобу Инубуши из Токийского научного университета (Япония) недавно предложила теоретическую схему. Они рассматривают процесс ПДР как проблему стабильности.
Соавторами сообщения, опубликованного в журнале Physical Review Letters 18 декабря 2023 года, являются профессор Йошитака Сайки из Университета Хитоцубаси, доцент Мики У. Кобаяси из Университета Риссё и профессор Сусумо Гото из Университета Осаки. Для этого исследовательская группа использовала междисциплинарный подход, объединив теорию хаоса и теорию синхронизации. Они сосредоточились на инвариантном многообразии, названном многообразием DA, и провели анализ устойчивости. Результаты показали, что критический масштаб длины является ключевым условием для DA; он характеризуется поперечными экспонентами Ляпунова (TLE), которые в конечном итоге диктуют успех или неудачу процесса DA. Кроме того, на основании недавнего открытия, показывающего зависимость максимальной экспоненты Ляпунова (LE) от числа Рейнольдса и связь TLEs с максимальной LE, они пришли к выводу, что критический масштаб длины увеличивается с ростом числа Рейнольдса, уточняя зависимость критического масштаба длины от числа Рейнольдса. Подчеркивая важность этих результатов, доктор Инубуши говорит:
Таким образом, предложенная теоретическая основа не только улучшает наше понимание турбулентности, но и открывает путь для новых методов, основанных на данных, которые могут повысить точность и надежность прогнозирования погоды. Фото: NASA 04.01.2024 |
Экология
 | |
| В экоиндексе городов Казани не нашлось места в первой тройке | |
Казань оказалась в рейтинге на четве... | |
 | |
| Natgeo: Источники кислорода на дне океана помогут искать жизнь во Вселенной | |
На дне Тихого океана, где нет с... | |
 | |
| JACS Au: Открыт метод переработки пластиковых отходов в электронные устройства | |
Университет штата Делавэр и Аргоннская на... | |
 | |
| Nature Energy: Создана мембрана для удаления CO2, работающая на влажности | |
Прямое улавливание воздуха — один и... | |
 | |
| Кристаллографы СПбГУ раскрыли структуру минерала, открытого более 70 лет назад | |
Учёные из международной группы, которую в... | |
 | |
| Applied Catalysis: MXene поможет получать экономически выгодный зеленый водород | |
137 стран мира подписали соглашение об из... | |
 | |
| На Дне аграрной науки в Казанском ГАУ представили около 30 новых проектов | |
10 июля в Агробиотехнопарке Казанского го... | |
 | |
| Сокращение выбросов оксида азота на фермах помогает климату и озоновому слою | |
Новое исследование, проведённое Университетом ... | |
 | |
| ME&E: Приложение для растений помогает определить последствия изменения климата | |
Известно, что растения реагируют на ... | |
 | |
| Геофизики СПбГУ займутся мобильными зондированиями мерзлоты на Ямале | |
Учёные Санкт-Петербургского госуда... | |
 | |
| Российские ученые нашли на Эльбрусе цинк и медь | |
Биологи изучили ледники Эльбруса, и ... | |
 | |
| Ноша последствий изменения климата ляжет на хрупкие женские плечи | |
Согласно новому исследованию, опубликованному ... | |
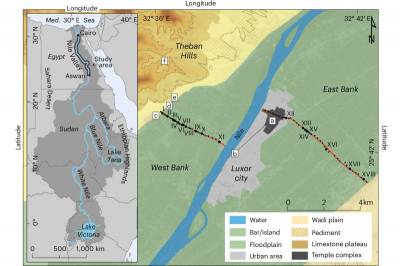 | |
| Nature Geoscience: Тысячелетия тому назад Нил был совсем другим | |
Исследователи изучили, как развивалась ре... | |
 | |
| Ученые впервые количественно оценили пробелы в удалении углерода | |
Новое исследование, проведенное Университетом ... | |
 | |
| Исследователи изучают влияние сольватации и валентности ионов на металлополимеры | |
В новой работе, опубликованной в журнале ... | |
 | |
| NREE: Виноградари всего мира бьют тревогу из-за изменения климата | |
Виноград, выращиваемый для производства в... | |
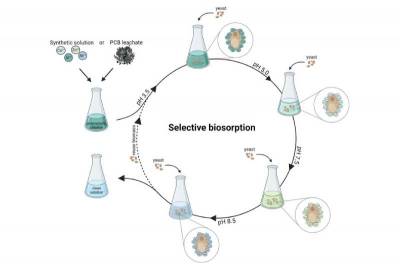 | |
| FB&B: Побочный продукт пива поможет перерабатывать металлические отходы | |
Когда мы перерабатываем электронные устро... | |
 | |
| Climate Dynamics: Вот как условия на суше влияют на муссонный климат Азии | |
Исследователи из Токийского столичного ун... | |
 | |
| Транзисторы на основе бальзового дерева усилят позиции зеленой электроники | |
Команда из Европы работает с деревом... | |
 | |
| Лесовосстановления недостаточно для возмещения углерода от заготовки древесины | |
Леса играют важнейшую роль в улавливании ... | |
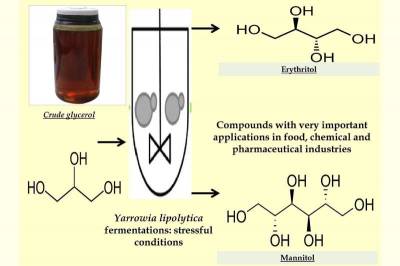 | |
| CRC: Сырой глицерин в качестве субстрата для дрожжей дает двойную выгоду | |
Использование сырого глицерина для синтез... | |
 | |
| Nature Comm: Солончаки и болота в 2 раза эффективнее смягчают парниковый эффект | |
Мангровые леса и солончаки поглощают боль... | |
 | |
| Functional Ecology: Чем разнообразнее лес, тем он лучше противостоит ураганам | |
Европейские леса с большим разнообразием ... | |
 | |
| Открытие позволит получать экологически чистый и экономически выгодный водород | |
Разработана прорывная технология, позволяющая ... | |
 | |
| Инновационный компонент очистителей воздуха обещает воздух без вредных примесей | |
Исследователи из Университета Бата изобре... | |
 | |
| Лаборатория Sandia нашла новые подсказки о потеплении в Арктике | |
Арктика, ледяная корона Земли, переживает клим... | |
 | |
| EHP: Изменение климата может повлиять на вес детей при рождении | |
Изменение климата может представлять большую о... | |
 | |
| Newswise: Потребители голосуют за консервативную, но не самую экологичную тару | |
Что бы вы предпочли скорее &mda... | |
 | |
| Natural Hazards: Смешанные леса защищают от цунами лучше монокультурных | |
Прибрежные леса в Японии преимущественно ... | |
 | |
| PRL: Новая концепция откроет тайны синхронизации в турбулентной динамике | |
Прогнозирование погоды важно для различны... | |